Die Musteraufgabe zum Höhensatz: Rechteck wird zu einem flächengleichen Quadrat
Wie konstruiert man ein fächengleiches Quadrat zu einem vorgegebenen Rechteck?
Dies ist eine Standard-Aufgabe zum Höhensatz im Rahmen des Themas Pythagoras in Klasse 8 oder 9, je nach Schulform.
In diesem Video zur Aufgabe aus dem Aufgabenblatt zeige ich euch wie es geht.
Die Powerpoint-Präsentation zu diesem Video könnt ihr mit online Zugang herunter laden.
Bitte beachten: es handelt sich um eine animierte Präsentation, d.h. die einzelnen Schritte seht ihr erst, wenn ihr die Präsentation aufruft und durchklickt!
Das Video zur Aufgabe: Recheck wird flächengleiches Quadrat
Die dazugehörige Powerpoint Präsentation könnt ihr euch im online Bereich herunter laden.
Die Lösungsschitte ausführlich:
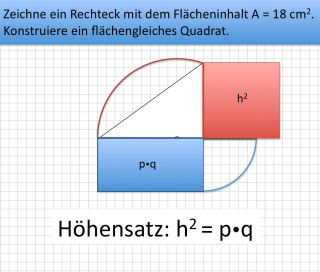
Zeichne das Rechteck. Zu jedem Flächeninhalt kann man ein geeignetes Rechteck finden. Immer kann man als eine Kantenlänge 1 cm wählen. Das Bild wird umso schöner, je näher die beiden Längen der Kanten eieinander liegen. Im Beispiel 18 Qudratzentimeter = 3 cm mal 6 cm.
Zeichne auf der rechten Seite des Rechtecks einen Kreisbogen mit dem Radius der senkrechten Kantenlänge ein.
Verlängere die waagerechte Kantenlänge des Rechtecks bis zum gerade gezeichneten Kreisbogen.
Finde nun die Mitte dieser neuen Strecke und trage einen Halbkreis über dem Rechteck ein.
Verlängere die senkrechte Kantenlänge des Rechtecks nach oben bis zum Halbkreisbogen.
Jetzt können wir ein rechtwinkliges Dreieck zeichnen. Wir erkennen die Höhe h und die beiden Hypotenusenabschnitte p ud q. p und q sind die ursprünglichen Kantenlängen des Rechtecks.
Es gilt jetzt h-Quadrat = p mal q. Das ist genau der Höhensatz, den wir schon kennen sollten.
Fragen zu diesem Thema? Dann diskutiert mit mir unter dem Video auf meinem Youtube-Kanal oder auf meiner Facebook-Seite mit mir!