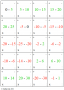
Lernspiel rationale Zahlen - rechnen mit negativen Zahlen in Klasse 6
Spielkarten + Würfel: Rechenkünstler rationale Zahlen kostenlos ausdrucken
Das Spiel wurde uns zur Verfügung gestellt von Frau Lotze - vielen Dank.
Wir rechnen mit negativen ganzen Zahlen und positiven ganzen Zahlen. Für das Lernspiel sollte mindestens eine Stunde eingeplant werden. Es bietet sich eine (Doppel-) Stunde direkt nach Einführung der negativen Zahlen an, da das Spiel mit kleinen negativen und positiven Zahlen arbeitet, die mit den Würfeln dargestellt werden können. Darauf aufbauend können komplexere Aufgaben und Rechnungen eingeführt werden.
Spielanleitung Lernspiel rationale Zahlen
Das Spielmaterial:
3 Würfel (ein Würfel mit Minuszahlen, einer mit Pluszahlen, einer gemischt)
20 Ergebniskarten
Ziel des Spiels:
Ziel des Spiels ist es, mindestens zwei der drei gewürfelten Zahlen mit Hilfe der vier Grundrechenarten so zu kombinieren, dass das Ergebnis im Zahlbereich der Ergebniskarte liegt.
Spielverlauf:
Zunächst wird mit den drei Würfeln gewürfelt und die drei Zahlen werden für alle Mitspieler gut sichtbar hingelegt. Danach wird eine Karte vom verdeckten Stapel umgedreht. Jetzt versuchen alle Spieler gleichzeitig, zwei oder alle drei gewürfelte Zahlen durch Addition, Subtraktion, Multiplikation oder Division so miteinander zu verbinden, dass das Ergebnis im Zielbereich liegt. Die Vorzeichen der gewürfelten Zahlen dürfen dabei nicht verändert werden. Wer zuerst eine Möglichkeit findet, ruft „Stopp“ und stellt seinen Rechenweg vor. Wenn dieser richtig ist, bekommt der Spieler die Karte. Sollte kein Spieler einen passenden Rechenweg, der zum Zielbereich führt, finden, werden die Würfel erneut geworfen. Wird nach dreimaligem Werfen kein passender Rechenweg gefunden, wird die Karte zur Seite gelegt und eine neue aufgedeckt. Wer zum Schluss die meisten Karten besitzt, hat das Spiel gewonnen.
Beispiel eines Spielverlaufs:
Die gewürfelten Zahlen sind -6; +1 und +4. Die Ergebniskarte zeigt den Zahlbereich 6-10.
Mögliche Rechenwege:
(+4) – (-6) = 10
(+4) – (–6) – (+1) = 9
(+4) – (-6) = 10 10 * (+1) = 10
Nicht möglich wäre (-6) * (-1) = 6, da das Vorzeichen der 1 nicht geändert werden darf.
Meine Würfel haben die Zahlen:
1. Würfel: -6; -5; -4; -3; -2; -1
2. Würfel: +1; +2; +3; +4; +5; +6
3. Würfel: -6; -4; -2; +1; +3, +5
Würfel mit negativen Zahlen erhält man im Internet oder am Besten kauft man "Blanko"-Holzwürfel, die selbst beschriftet werden können.
Würfel mit negativen Zahlen oder Blanko-Holzwürfel erhält man z.B. bei Edumero
Bastelbogen und Spielanleitung zum Lernspiel rationale Zahlen als PDF zum Ausdrucken
 Bastelbogen als PDF herunterladen
Bastelbogen als PDF herunterladen
 Spielanleitung "Rechenkünstler - lerne rationale Zahlen" als PDF herunterladen
Spielanleitung "Rechenkünstler - lerne rationale Zahlen" als PDF herunterladen