Binomische Formeln Herleitung (1. und 2. binomische Formel)

Herleitung der 1. Binomischen Formel

Herleitung der 2. Binomischen Formel

Binomische Formeln- anwenden und verstehen in Klasse 8

Was man über die binomischen Formeln wissen sollte (Klassenstufe 8/9)

Was sind binomische Formeln:

Die binomischen Formeln sind Merkformeln, die das Ausmultiplizieren von Klammerausdrücken erleichtern.

Daher findet man die binomischen Formeln immer im Zusammenhang mit Produkten von Summen und Differenzen.

Das sollte man schon wissen:

Flächenberechnung von Rechtecken und Quadraten:

Die Fläche eines Quadrates mit der Kantenlänge a beträgt: $A = a^2$

Die Fläche eines Rechtecks mit den beiden Kantenlängen a und b beträgt: $A = a \cdot b$

Ausmultiplizieren:

$a \cdot (b+c) = a \cdot b + a \cdot c$

$(a+b) \cdot c = a \cdot c + b \cdot c$

Der nächste Schritt zu den binomischen Formeln ist das Ausmultiplizieren des folgenden Terms: $(a+b) \cdot (c+d)$

sowie $(a+b) \cdot (a+b)$.

Multipliziere diese beiden Terme aus. Die Lösung findest du am Ende dieser Seite!

---

Die 3 Binomischen Formeln

Dies sind die binomischen Formeln, die im folgenden näher beschrieben und erläutert werden:

1. Binomische Formel:     $(a+b)^2=a^2 + 2ab+b^2$

2. Binomische Formel:     $(a-b)^2 = a^2 - 2ab + b^2$

3. Binomische Formel:     $(a+b) \cdot (a-b) = a^2 - b^2$

 

---

Die 1. Binomische Formel:

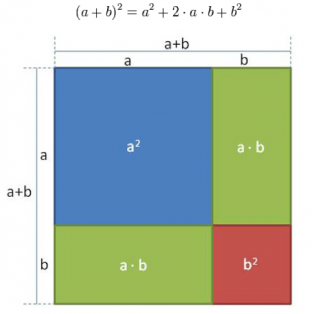
$(a+b)^2=a^2 + 2 \cdot a \cdot b + b^2$

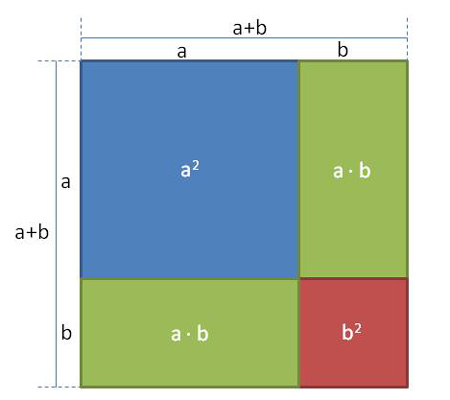
Das obige Quadrat hat die Kantenlänge (a+b). Man sieht direkt, dass ein Quadrat (blau) mit der Fläche a² sowie ein kleineres Quadrat (rot) der Fläche b² hineinpassen. Zusätzlich passen jedoch auch noch zwei gleich große Rechtecke (grün) hinein, die die Fläche a ⋅ b haben.

Im folgenden Bild ist dieser Zusammenhang nochmals dargestellt:

 

---

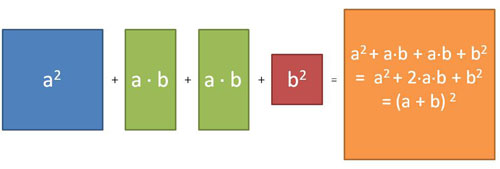
Die 2. Binomische Formel

 $(a-b)^2=a^2-2ab+b^2$

 

 

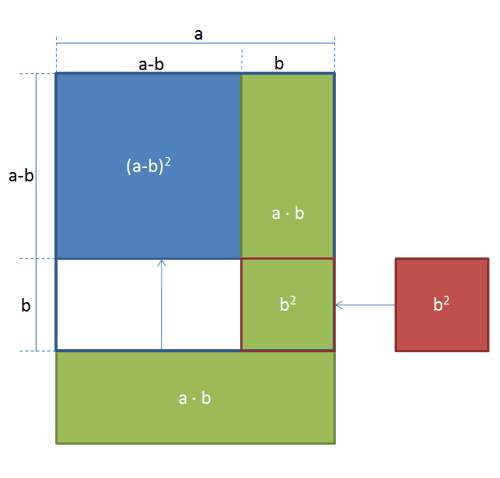
Wir nehmen an, das große Quadrat habe die Seitenlänge a. Wird diese um die Strecke b verkürzt, erhält man die Strecke (a-b).

Aus dem großen Quadrat erhalten wir das kleine mit der Seitenlänge (a-b), indem wir zweimal das Rechteck mit der Fläche a ⋅ b subtrahieren.Jetzt haben wir jedoch das kleine Quadrat mit der Kantenlänge b und der Fläche b² zuviel subtrahiert, daher müssen wir dieses wieder addieren: (a-b)² = a² - 2ab + b²

---

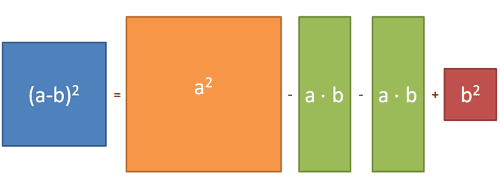
Lösung zu den Aufgaben am Anfang:

$(a+b) \cdot (c+d)= a \cdot c + a \cdot d + b \cdot c + b \cdot d$

$(a+b) \cdot (a+b) = a^2 + 2 \cdot a \cdot b + b^2$  (damit ist das die 1. Binomische Formel!)