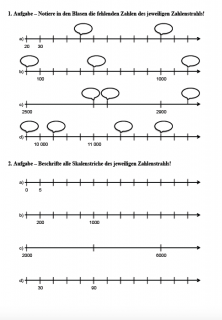
Zahlenstrahl Übungen - lernen, zeichnen Klasse 4 und Klasse 5
Zahlenstrahl - Erklärung, Beispiele und Arbeitsblätter
Der Zahlenstrahl dient als Anordnungselement für Zahlen und ein besseres Zahlenverständnis in der Mathematik. Der Zahlenstrahl ist eine gerade Linie, an der wir Zahlen anordnen können. In der Grundschule und der 5. Klasse ordnen wir an diesem geraden Strich nur natürliche Zahlen an. Später folgen dann auch negative Zahlen, Brüche, Dezimalzahlen und reelle Zahlen. Hier findest du Zahlenstrahl Übungen für die Klasse 4 und Klasse 5.
Quick Check - Zahlenstrahl Übungen als PDF einfach ausdrucken

 Zahlenstrahl Übungen: Arbeitsblätter Zahlenstrahl ausdrucken
Zahlenstrahl Übungen: Arbeitsblätter Zahlenstrahl ausdrucken
Vor den Zahlenstrahl Übungen: Das Lernvideo zum Zahlenstrahl anschauen!
Unser Lernvideo zum Zahlenstrahl - auf unserem YouTube-Kanal www.youtube.com/MathematikVideos bereitgestellt.
Zahlenstrahl oder Zahlengerade?
Der Zahlenstrahl wird manchmal auch Zahlengerade genannt. Mit den natürlichen Zahlen beginnt der Zahlenstrahl bei Null und ist genau genommen keine Gerade, weil er ja keine negativen Werte hat. Erweitern wir später den Zahlenstrahl um die negativen Zahlen, so wird es geometrisch genau betrachtet auch eine Gerade.
Wie zeichnet man einen Zahlenstrahl?
Wir zeichnen einen geraden Strich mit unserem Lineal und starten mit der Zahl Null am linken Ende unseres Zahlenstrahls. Hier befindet sich ein kleiner Strich und an diesem Strich oder genauer unter diesem Strich schreiben wir die Zahl Null. Nun wird es spannend. Wie legt man nun den Abstand bis zum nächsten Strich fest und welche Zahl ordnen wir hier an? Genau das wird entweder von der Aufgabe bereits vorgegeben oder du kannst es selbst bestimmen. Allerdings aufgepasst! Bei einem Zahlenstrahl sind die Abstände von einem Strich bis zum nächsten immer gleich groß. Einzige Ausnahme: es wurden absichtlich einige Striche weggelassen. Nehmen wir an, der Abstand von der Null zur Zahl 1 ist so groß wie in unserem Bild, dann müssen alle anderen Striche, die man Zahlenstriche oder auch Skalenstriche nennen kann, voneinander den gleichen Abstand haben:

An das Ende des Strichs zeichnen wir noch einen Pfeil. Das bedeutet, dass es hier eigentlich weiter geht, wir nur keinen Platz haben, es auf unserem Blatt zu zeichnen.
So sieht eine Zahlengerade für die Darstellung von negativen Zahlen aus:
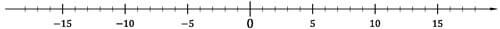
Wichtig hierbei ist, dass wir auf KEINEN Fall einen weiteren Pfeil an das linke Ende machen dürfen. Die Zahlen kommen aus dem negativen Bereich und werden immer größer nach rechts in den positiven Bereich bis ins Unendliche! Daher immer nur einen Pfeil an das rechte Ende machen!
Ein Zahlenstrahl hat folgende Eigenschaften:
- Er beginnt immer bei Null, auch wenn er ab einer anderen Zahl gezeichnet wird.
- Auf der rechten Seite befindet sich ein Pfeil
- Die Skalenstriche haben alle den gleichen Abstand
Warum sieht ein Zahlenstrahl nicht immer gleich aus?
Auf einem Zahlenstrahl sind ist jeweils vielleicht nur ein bestimmter Bereich interessant und daher wird nur der benötigte Bereich dargestellt. Je nach Zahlenbereich zeigt ein Zahlenstrahl nur einen kleinen Zahlenausschnitt oder einen großen Zahlenabschnitt. Wie man einen Zahlenstrahl dann skaliert erkläre ich euch im Video!
Zahlenstrahl 4 Klasse Arbeitsblätter PDF / Übungsblätter zum Zahlenstrahl zum Ausdrucken
Die hier vorgestellten Zahlenstrahl Arbeitsblätter sind Bestandteil des Übungsheftes "Mathestunde 5 - Grundrechenarten, Rechnen mit natürlichen Zahlen". Drucke die Zahlenstrahl Übungen aus und teste dein Wissen!
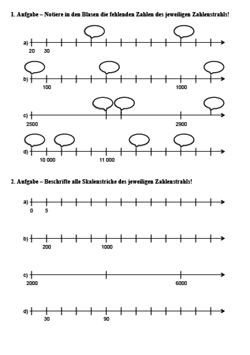 Arbeitsblatt zum Zahlenstrahl 1
Arbeitsblatt zum Zahlenstrahl 1  Arbeitsblatt zum Zahlenstrahl 2
Arbeitsblatt zum Zahlenstrahl 2