Bestimmung von PI mit der Monte-Carlo Methode
Der Kreis: Wir bestimmen die Kreiszahl Pi und die Fläche des Kreises
Mit verschiedenen Methoden hat man schon vor Jahrtausenden versucht, die Zahl PI zu berechnen. Ich stelle euch einige Methoden vor:
- Die Kuchenmethode, wir zerschneiden den Kreis
- Eine Simulation mit Excel oder einem Computerprogramm
Die Kuchenmethode
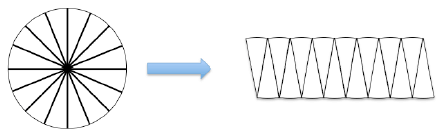
Wir zerlegen einen Kreis in gleich große Kuchenstücke und legen die Kuchenstücke abwechselnd
gegenseitig nebeneinander. Bei 16 Stücken ähnelt das neu gebildete Objekt schon sehr einem Rechteck.
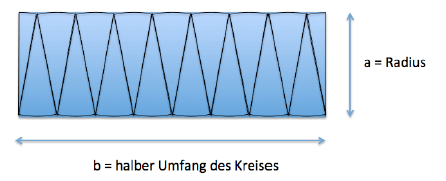
Das linke Stück halbieren wir nochmals und legen es an der rechten Seite an. Jetzt erhalten wir
schon fast ein Rechteck. Für unendlich viele Kuchenstücke erhalten wir als Fläche des Rechtecks:
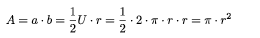
Dies ist exakt die Formel zur Berechnung der Fläche eines Kreises!
Die Monte-Carlo Methode zur Bestimmung der Kreiszahl PI
Mit dem Namen Monte-Carlo bzw. Monte-Carlo-Simulation verbindet man die Lösung von
mathematischen Problemstellungen mit Hilfe von Zufallszahlen.
Für die Berechnung der Kreisfläche oder auch der Zahl Pi beginnen wir mit einem Quadrat der
Fläche 1. Dieses Quadrat hat die Kantenlänge 1.
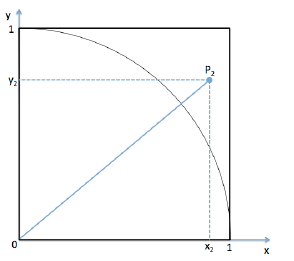
In dieses Quadrat zeichnen wir einen Viertelkreisbogen mit dem Radius 1 ein.
Wir erzeugen mit einem Zufallsgenerator beliebige Punkte innerhalb des Quadrats. Das bedeutet,
dass die Punkte innerhalb des Quadrats jeweils x- und y-Werte im Bereich von 0 bis 1 haben.
Bei mehreren tausenden solcher Punkte füllt sich das Quadrat mehr oder weniger gleichmäßig mit
diesen Punkten.
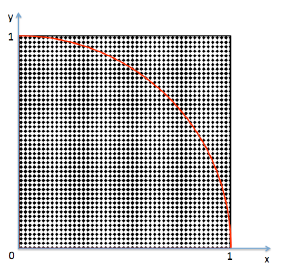
Wie man im Bild erkennen kann, befinden sich Punkte innerhalb des Viertelkreises und außerhalb.
Das Verhältnis der Anzahl der Punkte innerhalb des Viertelkreises zu der Anzahl der Punkte
insgesamt ist ein Maß für ein Viertel der Fläche des Kreises und damit zu einem Viertel der
Kreiszahl Pi.
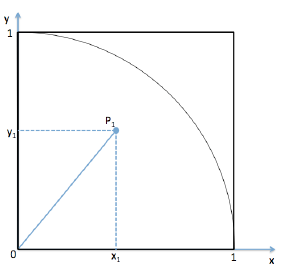
Wie können wir nun aus einzelnen x- und y-Werten den Abstand bestimmen?
Hierzu bestimmen wir den Abstand s des Punktes P vom Ursprung mit Pythagoras für den Punkt innerhalb des Kreises:
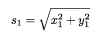
Und ausserhalb des Kreises:
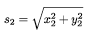
Man erhält Fläche des Viertelkreises aus dem Quotienten der Anzahl der Puntke innerhalb des Kreises durch die Anzahl der Punkte insgesamt.
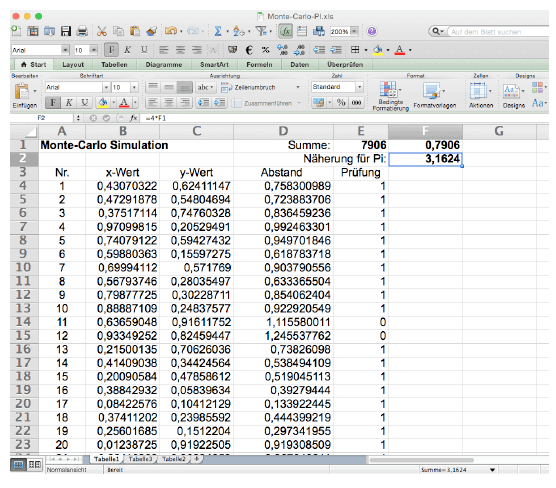
Eine Simulation mit Excel für 10000 Punkte ergibt z.B. 3,16... für die Zahl Pi.
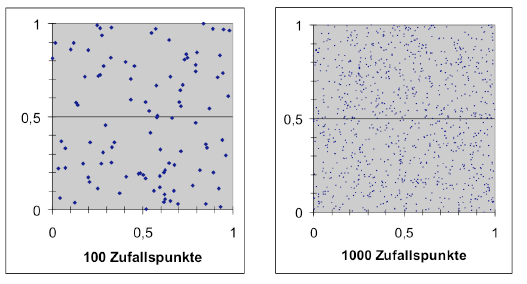
Die Punkte kann man sich auch grafisch dastellen lassen (Diagramm mit Excel, Typ: Punktdiagramm). Für 100 und 1000 Punkte erkennt man, dass die Fläche noch nicht gleichmäßig mit Punkten gefüllt ist:
Die Excel-Tabelle sowie das Skript kann mit online-Zugang herunter geladen werden.