Flächenberechnung Übungen Klasse 5
Arbeitsblätter Flächenberechnung
Flächeninhalte von Quadraten und Rechteckflächen bestimmen
6 Arbeitsblätter mit Lösungen zum Einstieg in das Thema:
Bewährte und in der Unterrichtspraxis eingesetzte Matheaufgaben von Mathefritz. Wir bestimmen den Flächeninhalt durch Zählen von Kästchen. 1 Kästchen entspricht einem Quadratzentimeter. Dreieckflächen können durch Verdopplung auf ein Quadrat oder Rechteck zurückgeführt werden. Diese Fläche muss dann wieder halbiert werden. Figuren werden ausgeschnitten und zusammengelegt. Rechtecke mit bekannten Seitenlängen werden berechnet. Alternativ kann der Flächeninhalt durch Zählen der Kästchen von 1 Quadratzentimeter bestimmt werden.
Quick Check - einfach ausdrucken!
Das Quadrat - Umfang und Flächeninhalt
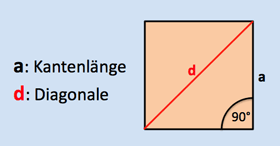
Umfang: $U = 4\cdot a$
Flächeninhalt: $A=a \cdot a=a^2$
Länge der Diagonalen: $d=a \cdot \sqrt{2}$
Definition und wichtige Formeln zum Quadrat (auswendig lernen!):
Ein Quadrat ist ein spezielles Viereck, bei dem alle Seiten gleich lang und alle Innenwinkel 90° betragen. Man kann auch sagen: „Ein Quadrat ist ein Rechteck mit 4 gleich langen Seiten“.
Weitere Eigenschaften:
- Gegenüber liegende Seiten sind parallel.
- Die Diagonalen sind gleich lang.
Die Kantenlänge ist eine Größe und wird mit einer Einheit angegeben!
Der Umfang ist das Vierfache der Kantenlänge, wir schreiben: $U =4 \cdot a$
Der Umfang eines Quadrats hat immer eine Längeneinheit.
Der Flächeninhalt ist das Quadrat der Kantenlänge a. Wir schreiben: $A = a^2$
Der Flächeninhalt hat immer als Einheit eine Länge zum Quadrat, z.B. $mm^2, cm^2, dm^2, m^2$.
Die Länge der Diagonalen kann mit Hilfe der Kantenlänge $a$ berechnet werden: $d=a \cdot \sqrt{2} \approx a \cdot 1,4$
Das Rechteck - Umfang und Flächeninhalt
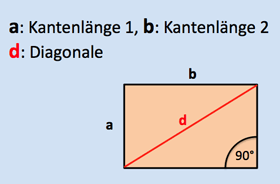
Umfang: $U = 2\cdot a + 2 \cdot b = 2 \cdot (a+b)$
Flächeninhalt: $A=a \cdot b$
Länge der Diagonalen: $d=\sqrt{a^2+b^2}$ (Satz des Pythagoras)
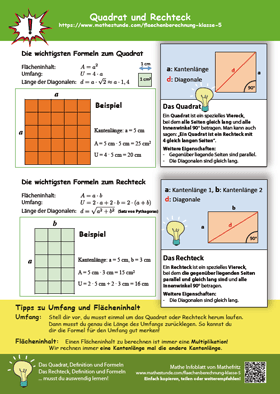
Das Infoblatt - Quadrat und Rechteck
Die Lernhilfe zum Thema Flächeninhalt und Umfang in Klasse 5 zum Ausdrucken.
Drucke das Blatt aus und nimm es mit als Lernhilfe in die Schule. Natürlich nicht zur Klassenarbeit, aber davor.
Gerne weitererzählen, weiterverteilen oder empfehlen!
Wichtiger Hinweis: Wenn beim Drucken die Option "KEINE SEITENANPASSUNG" gewählt wird, haben die kleinen Quadratzentimeter in den Beispielen auch eine echte Seitenlänge von 1 cm.
Muster Arbeitsblätter kostenlos zum ausdrucken






 Infoblatt Flächeninhalte ausdrucken
Infoblatt Flächeninhalte ausdrucken
