Differenzialrechnung Aufgaben – Üben und Lernen
Was ist die Differenzialrechnung?
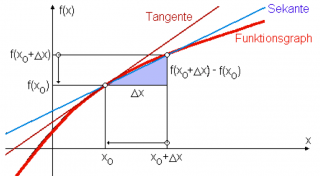
Die Differenzialrechnung ist ein Teilbereich der Analysis, der sich mit der Untersuchung von Änderungsraten befasst. Sie spielt eine zentrale Rolle in der Mathematik und ist besonders in der Naturwissenschaft und Technik von Bedeutung. Grundsätzlich geht es darum, wie sich Funktionen in einem bestimmten Punkt verändern. Zum Beispiel wird die Steigung einer Kurve durch die Ableitung bestimmt. In diesem Abschnitt erhältst du einen Überblick über die wichtigsten Konzepte und Begriffe der Differenzialrechnung.
Einführung in die Ableitungen
Ableitungen sind das Herzstück der Differenzialrechnung. Eine Ableitung gibt an, wie eine Funktion an einem bestimmten Punkt wächst oder sich ändert. In der Physik wird sie oft verwendet, um Geschwindigkeiten oder Beschleunigungen zu berechnen. Um die Differenzialrechnung zu verstehen, musst du die Regeln der Ableitung (wie die Produktregel, Kettenregel oder Quotientenregel) kennen. Hier findest du Aufgaben und Beispiele, die dir den Einstieg erleichtern.
Aufgaben zur Berechnung der ersten Ableitung
Die Berechnung der ersten Ableitung ist der erste Schritt in der Differenzialrechnung. In den folgenden Aufgaben lernst du, wie du die Ableitungen von einfachen und komplexen Funktionen berechnest. Finde die Ableitung folgender Funktionen und überprüfe deine Lösungen mithilfe der Lösungshinweise am Ende des Dokuments. Beispiele: \(f(x) = x^2 + 3x - 5\) und \(g(x) = 2e^x - \sin(x)\).
Extremstellen berechnen
Ein zentraler Bestandteil der Differenzialrechnung ist die Berechnung von Extremstellen, d.h. Hoch- und Tiefpunkten einer Funktion. Diese Punkte geben an, wo eine Funktion ihren maximalen oder minimalen Wert erreicht. Mit Aufgaben zu Extremstellen lernst du, wie du die Ableitungen verwenden kannst, um diese Punkte zu finden. In den Aufgaben wirst du lernen, wie man mithilfe der ersten und zweiten Ableitung auf Extremstellen schließen kann.
Wendepunkte und Krümmung berechnen
Wendepunkte und Krümmungen geben an, wie sich der Verlauf einer Funktion ändert. Wendepunkte sind Punkte, in denen der Graph seine Krümmung ändert. In diesem Abschnitt lernst du, wie du die zweite Ableitung verwenden kannst, um herauszufinden, wo solche Punkte liegen. Anhand der folgenden Aufgaben wirst du selbstständig Wendepunkte berechnen und verstehen, welche Rolle die zweite Ableitung dabei spielt.
Praktische Anwendungen der Differenzialrechnung
Die Differenzialrechnung hat viele praktische Anwendungen, von der Berechnung von Geschwindigkeiten und Beschleunigungen in der Physik bis hin zu Optimierungsaufgaben in der Wirtschaft. In den folgenden Aufgaben lernst du, wie du die Ableitung nutzen kannst, um reale Probleme zu lösen. Diese Beispiele helfen dir, die Mathematik besser zu verstehen und in praktischen Anwendungen anzuwenden.
Zusammenfassung der Differenzialrechnung
Zum Abschluss der Differenzialrechnung solltest du einen Überblick über die wichtigsten Konzepte und Regeln haben. Ableitungen, Extremstellen und Wendepunkte gehören zu den essenziellen Werkzeugen in der Mathematik. Diese abschließenden Aufgaben dienen zur Wiederholung und Festigung des Gelernten. Viel Erfolg!