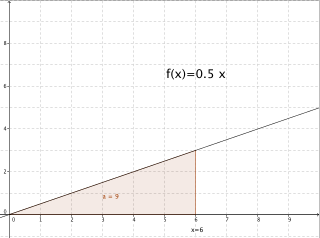
Die Methode der Ober- und Untersummen ist recht aufwändig. Daher versuchen wir zur Berechnung des Fächeninhalts unter einer Funktion eine andere Technik. Hierzu betrachten wir zunächst die Funktion f(x) = 0.5x.
Die Fläche darunter ist eine Dreiecksfläche und es gilt:
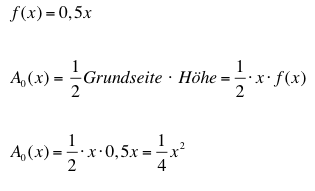
Für eine Parabel ist es nicht ganz so einfach und wir verwenden die Herleitung für die Obersumme mit n -> Unendlich:
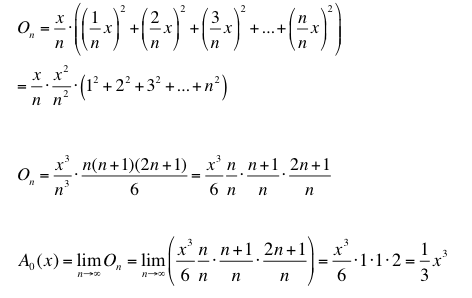
Wenn wir bei Null beginnen, können wir zur Berechnung der Fläche unter einer Geraden oder einer Parabel anstelle der aufwändigen Ober- und Untersummenberechnung eine einfache Funktion verwenden.
In unserem Beispiel für x = 3 ergibt sich als Flächeninhalt:
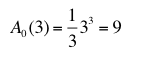
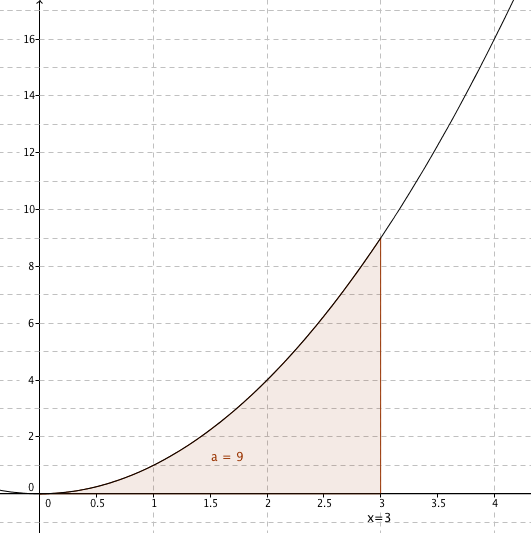
Jetzt fehlt uns noch der Zusammenhang zwischen dieser Flächenfunktion A(x) und der ursprünglichen Funktion f(x).
Arbeitsblatt mit weiteren Aufgaben zu diesem Thema und Lösungen im Downloadbereich.